Kurt Gödel’s Incompleteness Theorems are two groundbreaking results in the field of mathematical logic and the foundations of mathematics. These theorems were first published by Gödel in the early 20th century and had a profound impact on the philosophy of mathematics.
The Incompleteness Theorems can be summarized as follows:
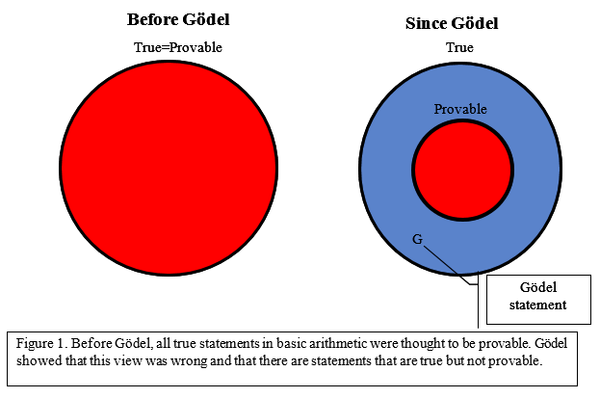
First Incompleteness Theorem: This theorem states that in any formal mathematical system that is sufficiently rich to include arithmetic (like Peano arithmetic), there exist statements that are true but cannot be proven within that system. In other words, there are mathematical propositions that can be stated, and we can intuitively understand that they are true, but there is no way to derive or prove them using the rules and axioms of that system.
Second Incompleteness Theorem: This theorem builds upon the first. It states that in a consistent formal mathematical system (one that doesn’t produce contradictions), the system cannot prove its own consistency. In other words, if a mathematical system is capable of proving that it is consistent, then it must be inconsistent.
These theorems have several important implications:
They show that there are limits to what can be achieved through formal mathematical reasoning. There will always be true mathematical statements that cannot be proven within a given system.
They demonstrate the limitations of attempting to establish the absolute foundation of mathematics. Gödel’s theorems imply that no single formal system can encompass all mathematical truths.
They raise questions about the relationship between mathematics and metamathematics. Gödel’s work showed that the study of mathematical systems is as important as the mathematics itself.
They have philosophical implications, challenging the idea that mathematics is an entirely closed and self-contained system. The theorems suggest that mathematics is more like an open-ended exploration with inherent limitations.
Gödel’s Incompleteness Theorems are considered some of the most important results in the philosophy of mathematics. They have led to extensive discussions about the nature of mathematical truth, the limits of formal systems, and the role of intuition and creativity in mathematics. These theorems also had a significant impact on computer science and logic, as they raise questions about the limits of what computers can prove or disprove.

